Compositional Generalization
Compositional generalization has a quite long history. However, I would like to briefly review recent works that caught my eye, and how important they are.
What is it?
Compositional Generalization is about can AI models generalize using different sub-knowledge in a compositional way to solve a more complex task? A simple example from the well-known benchmark SCAN is: “If you know JUMP, WALK, and WALK TWICE, you should be able to understand JUMP TWICE.” Conventional Seq2seq methods (as of 2020, uni-RNN, bi-RNN, Transformers) all failed dramatically in this task.
Why is it important?
Compositional generalization can be interpreted or is related to a lot of different fields, such as OOD robustness (generalization direction), disentaglement (compositional direction), logical reasoning, or distantly, transfer learning. Since each of them has shown remarkable successes in different fields, I think this task has not been as hot as it could be. Moreover, one of the “emergent abilities” of LLMs include showing traces of some level of compositional generalization ability, such as being able to translate from language A -> B when it has been only trained on A -> C and C -> B / B -> C pairs (forgot the source, will update 😅).
However, it is still an important task because it is what makes the AI reach human level reasoning. As Noam Chomsky puts it, human language has “infinite uses of finite means.” Humans compose finite set of meanings, tools, functions, etc. into infinite possibilities, which makes us creative.
Does Current LLM has it?
This is extensively explored by a recent UW paper: Faith and Fate: Limits of Transformer Compositionality. The short answer is: No.
Can Neural Networks do it?
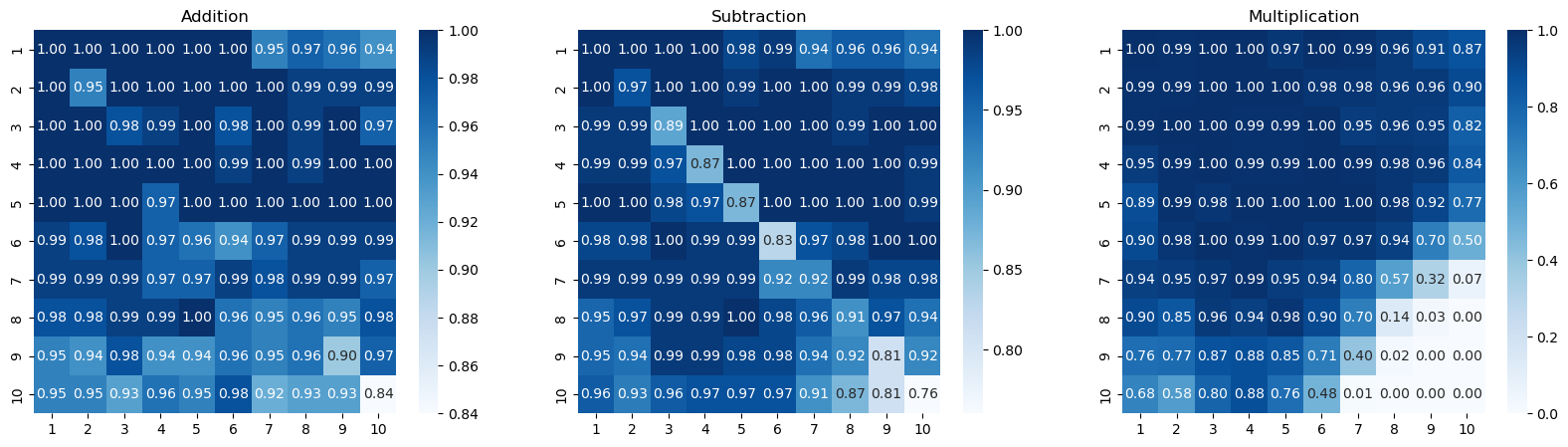
Yes and No. Some works such as LANE solve the SCAN generalization task to 100% accuracy. However, Teaching Arithmentics to Small Transformers shows that it fails to generalize for arithmetic in longer digits. Faith and Fate: Limits of Transformer Compositionality also shows that as the reasoning chain gets wider and deeper, Transformers (or similar auto-regressive sequence models) is likely to fail.
RWKV-4 Demo
A recent tweet from BlinkDL (developer of RWKV, a very cool project that builds 100% RNN-based LM!) showed that a small RWKV model can solve high-digit arithmetics, trained similarly (with reversed digit tricks) as in Teaching Arithmentics to Small Transformers.
I ran a quick experiment on it: (code link) can this generalize to longer digits? The findings suggest NO.
What do we need compositional generalization?
We don’t know it for sure yet. But, we know that simple MLE + Seq2Seq is not going to cut it. Either we need some auxiliary tasks, different loss, or different modules.